Answer:
y= -x
Explanation:
Slope-intercept form
y= mx +c, where m is the slope and c is the y-intercept
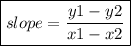
Slope


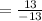

Substitute m= -1 into the equation:
y= -1x +c
y= -x +c
To find the value of c, substitute a pair of coordinates.
When x= -7, y= 7,
7= -(-7) +c
7= 7 +c
c= 7 -7
c= 0
Thus, the equation of the line is y= -x.