Answer:
1.13 hours after 12 noon or 4.13 hours after 9 A.M.
1:08 P.M. (rounded to the nearest minute)
Explanation:
To determine when the prices of the two stocks will be the same, we can set up equations for each stock's price as a function of time, t.
Let t represent the time in hours after 12 noon.
Stock A
The price of Stock A at 9 A.M. was $12.63, and it increases at the rate of $0.08 each hour. Therefore, at 12 noon it will be $12.87. So, the price of Stock A t hours after 12 noon can be represented as:
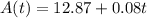
Stock B
The price of Stock B at noon was $13.13, and it decreases at the rate of $0.15 each hour. So, the price of Stock B t hours after noon. can be represented as:
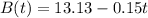
To find when the prices of the two stocks will be the same, we need to set A(t) equal to B(t) and solve for t:

Therefore, it will take approximately 1.13 hours after 12 noon for the prices of Stock A and Stock B to be the same. This translates to the time 1:08 P.M. (rounded to the nearest minute).