Explanation:
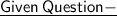
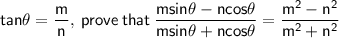

Given that
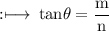
Now, Consider
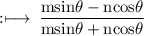
![\rm \: = \: (cos\theta\bigg[m(sin\theta)/(cos\theta) - n\bigg])/(cos\theta\bigg[m(sin\theta)/(cos\theta) + n\bigg])](https://img.qammunity.org/2022/formulas/mathematics/high-school/uokj92q32lkxbe3z95gvzo91a3auaatqkd.png)
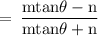
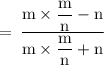
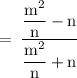
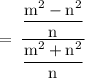
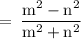
Hence,
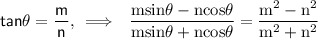
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
Additional Information:-
Relationship between sides and T ratios
sin θ = Opposite Side/Hypotenuse
cos θ = Adjacent Side/Hypotenuse
tan θ = Opposite Side/Adjacent Side
sec θ = Hypotenuse/Adjacent Side
cosec θ = Hypotenuse/Opposite Side
cot θ = Adjacent Side/Opposite Side
Reciprocal Identities
cosec θ = 1/sin θ
sec θ = 1/cos θ
cot θ = 1/tan θ
sin θ = 1/cosec θ
cos θ = 1/sec θ
tan θ = 1/cot θ
Co-function Identities
sin (90°−x) = cos x
cos (90°−x) = sin x
tan (90°−x) = cot x
cot (90°−x) = tan x
sec (90°−x) = cosec x
cosec (90°−x) = sec x
Fundamental Trigonometric Identities
sin²θ + cos²θ = 1
sec²θ - tan²θ = 1
cosec²θ - cot²θ = 1