Factorize the denominator:
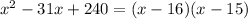
Then we find that ...
• When c = 15,
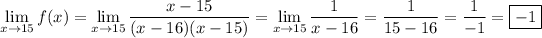
because the factors of x - 15 in the numerator and denominator cancel with each other. More precisely, we're talking about what happens to f(x) as x gets closer to 15, namely when x ≠ 15. Then we use the fact that y/y = 1 if y ≠ 0.
• When c = 16,
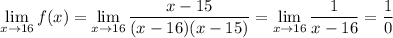
which is undefined; so this limit does not exist.
• When c = 17,
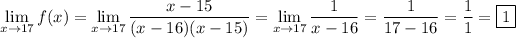
because the function is continuous at x = 17.