Question

Evaluate the limit:-


`\displaystyle \large{ \lim_(n \to \infty ) \frac{1 + {( - 3)}^(n) }{ {2}^(n) - {( - 3)}^(n) } }`
I am stuck on if I have to divide numerator and denominator by 3^n or (-3)^n.
Please show your work too — thanks!​

Answer 1

`\displaystyle \lim_(n\rightarrow \infty)\left[(1+(-3)^n)/(2^n-(-3)^n)\right]=-1`

Explanation:

Recall that when we are evaluating limits to infinity and negative infinity only, terms with a degree less than the highest degree are insignificant. Therefore, the 1 in the numerator is irrelevant as
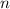`n` approaches infinity:

`\displaystyle \lim_(n\rightarrow \infty)\left[(1+(-3)^n)/(2^n-(-3)^n)\right]=\lim_(n\rightarrow \infty)\left[((-3)^n)/(2^n-(-3)^n)\right]`

Multiple by
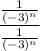`\displaystyle ((1)/((-3)^n))/((1)/((-3)^n))`:

`\displaystyle \lim_(n\rightarrow \infty)\left[((-3)^n)/(2^n-(-3)^n)\cdot ((1)/((-3)^n))/((1)/((-3)^n))\right]`

The numerator is
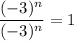`\displaystyle ((-3)^n)/((-3)^n)=1` and the denominator is
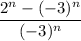`\displaystyle (2^n-(-3)^n)/((-3)^n)`. Simplify using
`\displaystyle (a-b)/(c)=(a)/(c)-(b)/(c)`:

`\displaystyle (2^n-(-3)^n)/((-3)^n)=(2^n)/((-3)^n)-((-3)^n)/((-3)^n)=(2^n)/((-3)^n)-1`

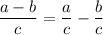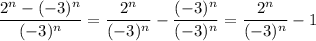
Thus we have:

`\displaystyle \lim_(n\rightarrow \infty)\left[((-3)^n)/(2^n-(-3)^n)\cdot ((1)/((-3)^n))/((1)/((-3)^n))\right]=\lim_(n\rightarrow \infty)\left[ (1)/((2^n)/((-3)^n)-1)\right]`

The limit of
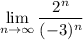`\displaystyle \lim_(n\rightarrow \infty) (2^n)/((-3)^n)` is simply 0 because the denominator grows faster than the numerator. The value varies from negative to positive as
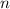`n` varies from being odd or even respectively, but it still approaches zero from both sides. Graphing might be unclear because the exponent in the denominator has a negative base, so
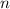`n` is only defined for all integers (
`n\in \mathbb{Z}`).

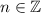Hence, we have:

`\displaystyle \lim_(n\rightarrow \infty)\left[((-3)^n)/(2^n-(-3)^n)\cdot ((1)/((-3)^n))/((1)/((-3)^n))\right]=\lim_(n\rightarrow \infty)\left[ (1)/((2^n)/((-3)^n)-1)\right]=(1)/(0-1)=(1)/(-1)=\boxed{-1}`