1 Answer

Stefan Novak · Answer 1 · 2022-09-19T23:06:42+0000

Answer:

4y - 5x + 7 = 0

Explanation:

To get to the equation of its perpendicular, firstly we'll need the slope of this line.

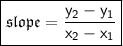
$\boxed{ \mathfrak{slope = \red{ \mathsf{ (y_(2) - y _(1))/(x_(2) - x _(1)) }}}}$

(x1, y1) and (x2, y2) are any two points kn the given line.

I caught two points that lie on this graph, and they are :

$\mathsf{ \implies \: slope = (y_(2) - y _(1))/(x_(2) - x _(1)) }$

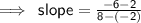
$\mathsf{ \implies \: slope = ( - 6- 2)/(8 - ( - 2)) }$

$\mathsf{ \implies \: slope = ( -8)/(8 + 2) }$

(two minus make a plus)

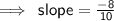
$\mathsf{ \implies \: slope = ( -8)/(10) }$

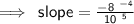
$\mathsf{ \implies \: slope = \frac{ \cancel{-8} {}^( \: \: - 4) }{ \cancel{10} \: \: {}^(5) } }$

slope = -4 /5

That's the slope of the given line.

Now, the slope of the line perpendicular to this one will be equal to its negative reciprocal.

slope (perpendicular) = 5/ 4

and they've given a point that lies in the perpendicular, it is = (3, 2)

For equation of a line thru a point, we have:

$\boxed{ \mathsf{ \red {y} - {y}^(1) = slope * (\red{x} - {x}^(1) }) }$

the letters in red are the variables that won't be changed thruout.

and (x¹, y¹) are the points on the line.

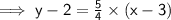
$\implies \mathsf{y - 2 = (5)/(4) * (x - 3) }$

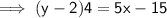
$\implies \mathsf{(y - 2)4 = 5x - 15}$

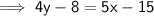
$\implies \mathsf{4y - 8 = 5x - 15}$

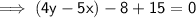
$\implies \mathsf{(4y - 5x) - 8 + 15 = 0}$

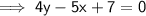
$\implies \mathsf{4y - 5x + 7 = 0}$

and thats the required equation of the perpendicular.

Please log in or register to add a comment.