If
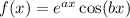
then by the product rule,
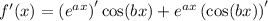
and by the chain rule,
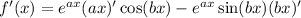
which leaves us with

Alternatively, if you exclusively want to use the chain rule, you can carry out logarithmic differentiation:
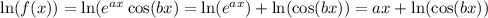
By the chain rule, differentiating both sides with respect to x gives
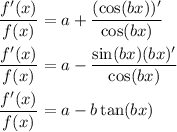
Solve for f'(x) yields
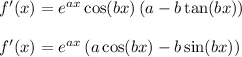
just as before.