Question

Find the derivative of f(x)= (e^ax)*(cos(bx)) using chain rule

Answer 1

If

`f(x) = e^(ax)\cos(bx)`

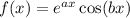
then by the product rule,

`f'(x) = \left(e^(ax)\right)' \cos(bx) + e^(ax)\left(\cos(bx)\right)'`

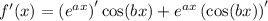
and by the chain rule,

`f'(x) = e^(ax)(ax)'\cos(bx) - e^(ax)\sin(bx)(bx)'`

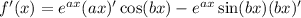
which leaves us with

`f'(x) = \boxed{ae^(ax)\cos(bx) - be^(ax)\sin(bx)}`

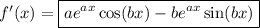
Alternatively, if you exclusively want to use the chain rule, you can carry out logarithmic differentiation:

`\ln(f(x)) = \ln(e^(ax)\cos(bx)} = \ln(e^(ax))+\ln(\cos(bx)) = ax + \ln(\cos(bx))`

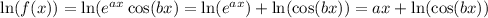
By the chain rule, differentiating both sides with respect to x gives

`(f'(x))/(f(x)) = a + ((\cos(bx))')/(\cos(bx)) \\\\ (f'(x))/(f(x)) = a - (\sin(bx)(bx)')/(\cos(bx)) \\\\ (f'(x))/(f(x)) = a-b\tan(bx)`

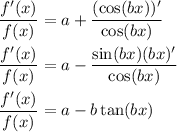
Solve for f'(x) yields

`f'(x) = e^(ax)\cos(bx) \left(a-b\tan(bx)\right) \\\\ f'(x) = e^(ax)\left(a\cos(bx)-b\sin(bx))`

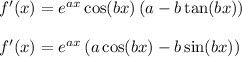
just as before.