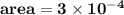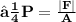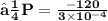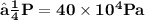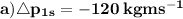
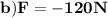
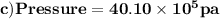
__________________________________________
❒ To find the change in momentum for bullets , we need to remember the momentum p of a bullet is equal to product of mass and speed
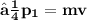
❒ This means , that change in momentum for one bullet will be equal to
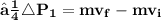
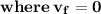
Total change in momentum for the bullet in 10 sec is equal to product of change in momentum for one bullet and number of bullets hit the wall in 10 sec
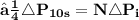
❒ Note :-
Change in momentum given is the change of momentum in 10 sec is 10 times less
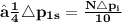
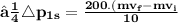
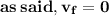
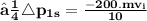
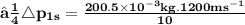
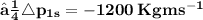
__________________________________________
b) to find average force F on the wall we must remember that in general case force us the change of momentum in time :
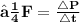
Total change of momentum of bullets in 10 sec
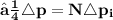
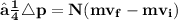
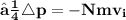
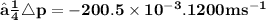
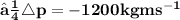
❒ We can find total force exerted in the wall in 10sec by dividing the momentum of bullet with 10 sec
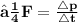
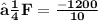
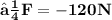
__________________________________________
c) To find average pressure :