Question

Which point gives the vertex of f(x) = -x2 + 4x - 3?

A) (2,-1)
B) (2.1)
C) (2,-13)
D) (-2,-13)

Answer 1

B (2.1)

Explanation:

it was on a test i got it right

Answer 2

B

Explanation:

There are several ways to find the vertex of function such as formula, completing the square or differential.

I will use the formula to find the vertex.

We are given the function:

`\displaystyle \large{f(x) = - {x}^(2) + 4x - 3}`

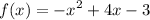
Vertex Formula

Let (h,k) = vertex

`\displaystyle \large{ \begin{cases} h = - (b)/(2a) \\ k = \frac{4ac - {b}^(2) }{4a} \end{cases}}`

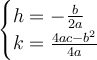
From the function, compare the coefficients:

`\displaystyle \large{a {x}^(2) + bx + c = - {x}^(2) + 4x - 3}`

• a = -1
• b = 4
• c = -3

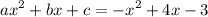
Therefore:-

`\displaystyle \large{ \begin{cases} h = - (4)/(2( - 1)) \\ k = \frac{4( - 1)( - 3)- {4}^(2) }{4( - 1)} \end{cases}}`

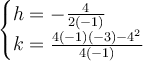
Then evaluate for h-value and k-value.

`\displaystyle \large{ \begin{cases} h = - (4)/( - 2) \\ k = (4( 3)- 16)/( - 4) \end{cases}} \\ \displaystyle \large{ \begin{cases} h = 2 \\ k = (12 - 16)/( - 4) \end{cases}} \\ \displaystyle \large{ \begin{cases} h = 2 \\ k = ( - 4)/( - 4) \end{cases}} \\ \displaystyle \large{ \begin{cases} h = 2\\ k = 1\end{cases}}`

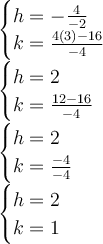
Therefore the vertex is (h,k) = (2,1)