Explanation:
Given Question :-
Solve for x :-
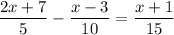

Given linear equation is
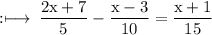
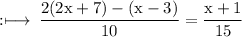
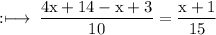
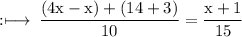
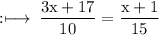
On multiply by 5 on both sides,
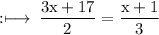
On cross multiplication, we get
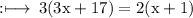
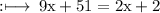
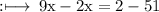
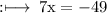
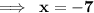
VERIFICATION
Consider, LHS
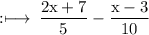
On substituting the value of x, we get
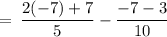
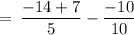
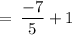
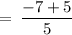
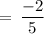
Consider RHS
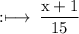
On substituting the value of x, we get
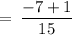
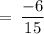
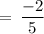
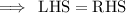
HENCE, VERIFIED