Answer:
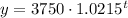
(where
 is the population and
is the population and
 is time in years after 2021)
is time in years after 2021)
5159
Explanation:
Part (a)
General form of an exponential function:

where:
 is the y-intercept (or initial value)
is the y-intercept (or initial value)
 is the base (or growth factor) in decimal form
is the base (or growth factor) in decimal form
 is the independent variable
is the independent variable
If
 then it is an increasing function
then it is an increasing function
If
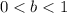 then it is a decreasing function
then it is a decreasing function
We are told that the initial population is 3750. Therefore,
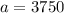
We are told that the farm grows at a rate of 2.15% annually. Therefore, if it grows then every year it is 100% + 2.15% = 102.15% of the previous year.
Convert the percentage into a decimal:
102.15% = 102.15/100 = 1.0215
Therefore,
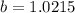
We are told that the independent variable is
 (in years).
(in years).
Therefore, the equation is
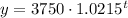
(where
 is the population and
is the population and
 is time in years after 2021)
is time in years after 2021)
------------------------------------------------------------------------------------------
Part (b)
The year 2036 is 15 years after 2021. Therefore, substitute
 into the equation and solve for
into the equation and solve for
 :
:


Therefore, an estimate of the population of the town in 2036 is 5159.