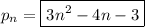Question

Please help, What is the nth term rule of the quadratic sequence below?
-4,1,12,29,52,81,116

Answer 1

If the sequence is quadratic, then the n-th term (n ≥ 1) is

`p_n = an^2 + bn + c`

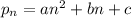
We're given the first four terms,

`\begin{cases}p_1=-4\\p_2=1\\p_3=12\end{cases}`

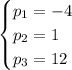
Using the formula for the n-th term, this turns into a system of equations,

`\begin{cases}a+b+c=-4\\4a+2b+c=1\\9a+3b+c=12\end{cases}`

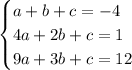
Solve the system:

• Eliminate c :

(4a + 2b + c) - (a + b + c) = 1 - (-4) ===> 3a + b = 5

(9a + 3b + c) - (a + b + c) = 12 - (-4) ===> 8a + 2b = 16

• Multiply the second equation by 1/2 to get 4a + b = 8, then eliminate b and solve for a :

(4a + b) - (3a + b) = 8 - 5 ===> a = 3

• Solve for b and c :

3a + b = 9 + b = 5 ===> b = -4

a + b + c = 3 - 4 + c = -4 ===> c = -3

Then the rule for the n-th term is

`p_n = \boxed{3n^2 - 4n - 3}`