Question

What does 4^8/4^-2 equal?

Answer 1

4^10 (base 4)

2^20 (base 2)

Explanation:

Law of Exponent:

`\displaystyle \large{ \frac{ {a}^(m) }{ {a}^(n) } = {a}^(m - n) }`

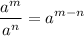
Compare:

`\displaystyle \large{ \frac{ {a}^(m) }{ {a}^(n) } = \frac{ {4}^(8) }{ {4}^( - 2) } }`

• a = 4
• m = 8
• n = -2

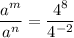
Therefore:

`\displaystyle \large{ \frac{ {4}^(8) }{ {4}^( - 2) } = {4}^(8 - ( - 2)) } \\ \displaystyle \large{ \frac{ {4}^(8) }{ {4}^( - 2) } = {4}^(8 + 2) } \\ \displaystyle \large{ \frac{ {4}^(8) }{ {4}^( - 2) } = {4}^(10) }`

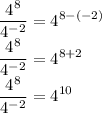
Althought you didn't specific if I should leave answer as base 4 or base 2.

If you want the answer in base 2.

From:

`\displaystyle \large{ {4}^(10) = { ({2}^(2)) }^(10) }`

Law of Exponent II

`\displaystyle \large{ { ({a}^(m) )}^(n) = {a}^(m * n) }`

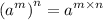
Apply the law:

`\displaystyle \large{ {4}^(10) = { ({2}^(2)) }^(10) } \\ \displaystyle \large{ {4}^(10) = {2}^(20) }`

Thus, in base 2 form, it's 2^20