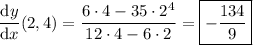Given that
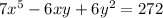
differentiating both sides with respect to x (using the power, product, and chain rules) yields
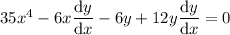
Solving for dy/dx gives
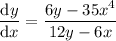
This gives the slope of the tangent line to the curve at any point (x, y). In particular, the slope of the tangent to (2, 4) is