Explanation:
★ Solution :-
To find the value of x, we use a concept called as "The sum of interior angles on same side of transversal always measures 180° when added together".
Value of x :-
According to the concept,

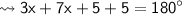
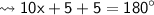
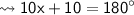
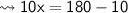
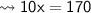
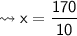
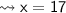
Now, let's find each of the angles.
Measurement of first angle :-
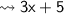
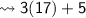

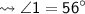
Measurement of second angle :-
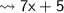
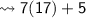

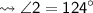
Measurement of third angle :-
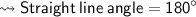
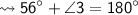
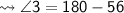
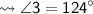
Measurement of fourth angle :-


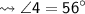
Therefore, the ∠1, ∠2, ∠3 and ∠4 measures 56°, 124°, 56° and 124° respectively. The value of x is 17.