Answer:
![\displaystyle \lim_(n\rightarrow \infty)\left[(1)/(n)\cos\left((n\pi)/(3)\right)\right]=0](https://img.qammunity.org/2022/formulas/mathematics/high-school/iq8meh6ui0fi4xer1h5a5gywipq9yacelt.png)
Explanation:
The squeeze theorem states that if
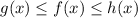 for all
for all
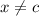 in some interval around
in some interval around
 and
and
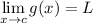 and
and
 , then it follows that
, then it follows that
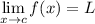 .
.
Essentially what this is saying is that if a function
 is always smaller than or equal to function
is always smaller than or equal to function
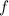 in some interval and a function
in some interval and a function
 is always greater than or equal to
is always greater than or equal to
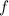 in the same interval, if
in the same interval, if
 and
and
 approach the same value at some point,
approach the same value at some point,
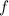 must also approach that point, since it is being "squeezed", hence the name squeeze theorem.
must also approach that point, since it is being "squeezed", hence the name squeeze theorem.
Recall that the maximum output of cosine is 1 and the minimum output of cosine is -1. A quick check on the unit circle will confirm this.
Therefore, the function
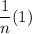 will always be greater than or equal to
will always be greater than or equal to
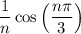 and the function
and the function
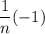 will always be less than or equal to
will always be less than or equal to
 .
.
Hence,
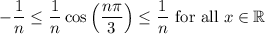 .
.
We can easily compute
![\displaystyle \lim_(n\rightarrow \infty)\left[- (1)/(n)\right]](https://img.qammunity.org/2022/formulas/mathematics/high-school/qw66bup7s8enej6cnnq4vujtk8hbdpzx9x.png) and
and
![\displaystyle \lim_(n\rightarrow \infty)\left[(1)/(n)\right]](https://img.qammunity.org/2022/formulas/mathematics/high-school/rmld9zuz2oh56mqfis8w2p6cd4r7uuksvr.png) with direct substitution.
with direct substitution.
Therefore, we have:
![\displaystyle \lim_(n\rightarrow \infty)\left[- (1)/(n)\right]=-(1)/(\infty)=0\\\\\displaystyle \lim_(n\rightarrow \infty)\left[ (1)/(n)\right]=(1)/(\infty)=0](https://img.qammunity.org/2022/formulas/mathematics/high-school/rn3hv16bnejdii26xk2vag0s9lnmxv7l39.png)
Since
![\displaystyle \lim_(n\rightarrow \infty)\left[- (1)/(n)\right]=\displaystyle \lim_(n\rightarrow \infty)\left[ (1)/(n)\right]=0](https://img.qammunity.org/2022/formulas/mathematics/high-school/yus2e6gp78xw73fwu99pqk9oiaib9df9a7.png) and
and
 , then from the squeeze theorem,
, then from the squeeze theorem,
![\displaystyle \lim_(n\rightarrow \infty)\left[(1)/(n)\cos\left((n\pi)/(3)\right)\right]= \lim_(n\rightarrow \infty)\left[- (1)/(n)\right]=\displaystyle \lim_(n\rightarrow \infty)\left[ (1)/(n)\right]=\boxed{0}](https://img.qammunity.org/2022/formulas/mathematics/high-school/fpg6zh3h4ukhyifb8zoeeikl40negidn6r.png)