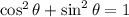Answer:
Explanation
There are many ways to prove this identity. But, I will use the simplest one. If you have a right triangle, the length of the horizontal side is x, the length of the vertical side is y, and the hypotenuse is r. So, the relation between x and r can be written in cosine form:
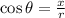
The relation between y and r can be written in sine form:
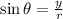
Pythagoras told you that for the right triangle
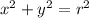 should be satisfied. Substitute x and y from the cosine and sine form:
should be satisfied. Substitute x and y from the cosine and sine form:

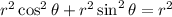
the square of r will cancel out, and you can get your identity: