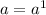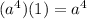Answer:
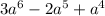
Explanation:
Use the rules of indices to find the product.
One of the rules is that when we multiply indices that have the same base we add the powers. For example:
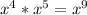
So to work out
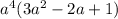 we need to follow this rule.
we need to follow this rule.
Let's expand the bracket:
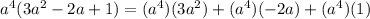
Let's simplify keeping in mind the rule we know.
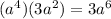
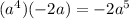 - remember that
- remember that