Answer:
It is not a solution.
Explanation:
First, as we know what x is equal to, substitute the second equation into the first:
3x + 2y = 27
3(y + 1) + 2y = 27
3y + 3 + 2y = 27
5y + 3 = 27
Subtract 3 from both sides:
5y + 3 - 3 = 27 - 3
5y = 24
Divide both sides by 5:

So
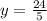
At this point we know that (5, 6) is not a solution to the system because this should be the y value (6). To confirm this we will calculate x by substituting in the known y in the second equation:
x = y + 1
x =
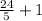
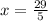
Further proving that (5,6) is not a solution.
Hope this helps!