Question

g A 38-g ball at the end of a string is swung in a vertical circle with a radius of 21 cm. The tangential velocity is 200.0 cm/s. Find the tension in the string:

Answer 1

It depends on the location of the ball during the motion. The string tension are approximately 3.82 N (at the lowest point), 3.06 N (at the highest point), and 3.44 N (at the horizontal point).

Step-by-step explanation:

Tension in the String can be determined by the Newton's 1st Law of Motion (The ball shouldn't be escaped from the trajectory). The value of
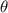`\theta` indicates the angle that is measured from the vertical lines and the rope of length R)

`\sum F=0\rightarrow (mv^(2))/(R)+mg\cos\theta-T=0`

`T=mg\cos\theta+(mv^(2))/(R)`

`T=(38*10^(-3))(10)(\cos\theta)+(38*10^(-3))(2^(2))/(0.21^(2))=0.38\cos\theta+3.44`

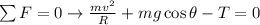
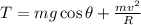
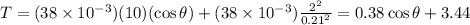
When the ball is at the lowest point, the value of angle
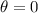`\theta=0`, so the string tension is approximately 3.82 N. If the ball is at the highest point the value of
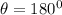`\theta=180^(0)`, so the string tension is approximately 3.06 N, and at the horizontal point
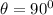`\theta=90^(0)`, so the string tension is approximately 3.44 N.