Answer:
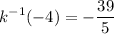
Explanation:
We are given the function:
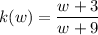
And we want to find k⁻¹(-4).
Recall that by the definition of inverse functions:
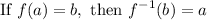
Let k⁻¹(-4) = x, where x is an unknown value. Then by definition, k(x) must equal -4.
So:

Solve for x:
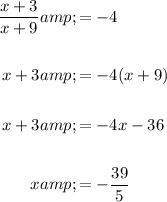
Hence, k(-39/5) = -4. By definition of inverse functions, then, k⁻¹(-4) = -39/5.