Answer:
It depends on the location of the ball during the motion. The string tension are approximately 3.82 N (at the lowest point), 3.06 N (at the highest point), and 3.44 N (at the horizontal point).
Step-by-step explanation:
Tension in the String can be determined by the Newton's 1st Law of Motion (The ball shouldn't be escaped from the trajectory). The value of
 indicates the angle that is measured from the vertical lines and the rope of length R)
indicates the angle that is measured from the vertical lines and the rope of length R)
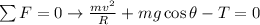
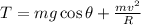
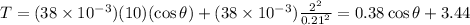
When the ball is at the lowest point, the value of angle
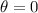 , so the string tension is approximately 3.82 N. If the ball is at the highest point the value of
, so the string tension is approximately 3.82 N. If the ball is at the highest point the value of
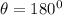 , so the string tension is approximately 3.06 N, and at the horizontal point
, so the string tension is approximately 3.06 N, and at the horizontal point
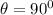 , so the string tension is approximately 3.44 N.
, so the string tension is approximately 3.44 N.