Answer:
Slope of AC = -1/4
Slope of BD = 2
AC is not perpendicular to BD.
Explanation:
Given the following points:
A (2, 1) & C (-2, 2)
B (-1, 4) & D (-3, 0)
Plug these values into the slope formula:
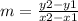
Let A = (x1, y1), & C = (x2, y2)
B = (x1, y1), & C = (x2, y2)
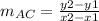
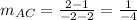
Therefore, the slope of AC = -1/4.
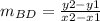

Therefore, the slope of BD = 2.
By definition, perpendicular lines have slopes that are negative reciprocals. This means that when you multiply the slopes of those two lines, it will result in - 1.
By multiplying the slopes of AC and BD, you'll get:
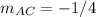 ×
×
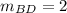 = -1/2
= -1/2
Since the product of the slopes of AC and BD is -1/2, then it means that their lines are not perpendicular because the product of their slopes is not equal to -1.