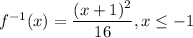Question

1. For the Function f(x)= -4 sqrt x-1, find the inverse function.

2. The function f(x)=(x-1)^2-4 is not-one-to-one. If you restrict the domain f(x) to x (less or equal) 1, what is it’s inverse function and the domain for the inverse?

Answer 1

9514 1404 393

Answer:

`f^(-1)(x)=((x+1)^2)/(16),x\le-1`

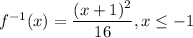
Explanation:

The domain of the inverse function is the range of the function. Function values for x ≥ 0 will be -1 or less, Hence the domain of the inverse function will be x ≤ -1.

In order to match the function's domain of x ≥ 0, the range of the inverse function must be non-negative values. Hence there can be no minus sign in front of the squared expression. The inverse function must be ...

`f^(-1)(x)=((x+1)^2)/(16),x\le-1`