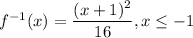9514 1404 393
Answer:
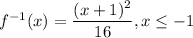
Explanation:
The domain of the inverse function is the range of the function. Function values for x ≥ 0 will be -1 or less, Hence the domain of the inverse function will be x ≤ -1.
In order to match the function's domain of x ≥ 0, the range of the inverse function must be non-negative values. Hence there can be no minus sign in front of the squared expression. The inverse function must be ...