Answer:
m = 10
Explanation:
We are going to use sine ratio as sine ratio is opposite to hypotenuse.
We know the value of opposite which is 5√3
The value of hypotenuse is m which is unknown.
Therefore:-
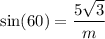
We know that sin60° is √3/2
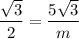
Multiply both sides by LCM which is 2m.

Divid both sides by √3 to isolate m.
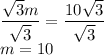
And we're done! The value of m is 10.
Alternative Solutions
If we do not want to use sin60°, we can use cos30°.
Focus the 30°, since for 30°, 5√3 is adjacent and m is hypotenuse.
cosine ratio is adjacent to hypotenuse.
Therefore:-

We know that cos30° is √3/2
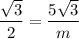
Notice something? Both equations when we use sin60° and cos30° are same. This is called a co-function.
Since sin60° = cos30°, both methods work.
If we do not want to use sin60°, you can use cos30°.