Question

Find the sum of each sequence.

31,41,51,61,71,81,91,101

Group of answer choices

417

528

639

427

Answer 1

528

Explanation:

We are given the following sequence:

31,41,51,61,71,81,91,101

Count the terms and see that there are 8 terms total.

If you notice, each terms add up by 10.

31+10 = 41

41+10 = 51

51+10 = 61

Therefore, this is an arithmetic sequence with 10 as common difference.

To find the sum of 8 sequences, we will be using the following formula.

`\displaystyle \large{S_n = (1)/(2) n(a_1 + a_n)}`

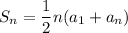
We know that:

• There are 8 terms total. (n = 8)
• Our first term is 31 (a1 = 31)
• Our last term is 101 (an = 101)

Substitute the following in the sum formula.

`\displaystyle \large{S_8 = (1)/(2) (8)(31+ 101)} \\ \displaystyle \large{S_8 = 4(132)} \\ \displaystyle \large{S_8 = 528}`

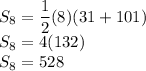
Therefore, the sum of all 8 sequences is 528.