Question

Please complete the details of your answer

please help me please​

Answer 1

`\huge \boxed{\mathbb{QUESTION} \downarrow}`

• Solve the following word problems.

`\large \boxed{\mathbb{ANSWER\: WITH\: EXPLANATION} \downarrow}`

Question 1 ↴

➜ Area of the lot = 2x² + 7x + 3 cm²

➜ Width of the garden = 2x + 1 cm.

➜ Length of the garden = y

﹋﹋﹋﹋﹋

✪ Area of a rectangle = length × width

⇒ length = area ÷ width

⇒ y = 2x² + 7x + 3 ÷ 2x + 1

﹋﹋﹋﹋﹋

WORKING ↷

`\tt \: y = \frac{ {2x}^(2) + 7x + 3}{2x + 1} \\ \\ \sf \: Factorise \: {2x}^(2) + 7x + 3. \\ \\ \tt \: y = (\left(x+3\right)\left(2x+1\right))/(2x+1) \\ \\ \sf \: Cancel \: out \:( 2x + 1 )\\ \\ \large\boxed{\boxed{\bf y = x+3 }}`

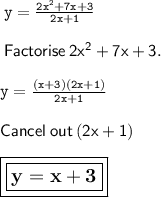
✯ Length of the garden = x + 3 cm.

▨▧▨▧▨▧▨▧▨▧▨▧▨▧▨▧▨

Question 2 ↴

➜ Area of the frame = 4x² - 4xy + y² cm²

➜ Length of the side of the frame = s

﹋﹋﹋﹋﹋

✪ Area of a square = side²

⇒ 4x² - 4xy + y² = s²

﹋﹋﹋﹋﹋

WORKING ↷

`\tt {4x}^(2) - 4xy + {y}^(2) = {s}^(2) \\ \\ \sf \: Use \: the \: algebraic \: identity \downarrow \: \\ \sf {a}^(2) - 2ab + {b}^(2) = (a - b) ^(2) ... \\ \sf \: a = 2x \: and \: b = y \\ \\ \tt \left(2x-y\right)^(2) = {s}^(2) \\ \\ \sf \: Squaring \: on \: both \: the \: sides \\ \\ \tt \sqrt{(2x - y) ^(2) } = \sqrt{ {(s)}^(2) } \\ \large\boxed{\boxed{\bf \: (2x - y) = s}}`

✯ Length of the side of the frame = 2x - y cm.

▨▧▨▧▨▧▨▧▨▧▨▧▨▧▨▧▨

Question 3 ↴

➜ Length of the rectangle = x + 5 cm

➜ Width of the garden = x + 3 cm.

➜ Area of the garden = a

﹋﹋﹋﹋﹋

✪ Area of a rectangle = length × width

⇒ a = (x + 5) × (x + 3)

﹋﹋﹋﹋﹋

WORKING ↷

`\tt \: a = (x + 5) * (x + 3) \\ \\ \sf \: multiply \: (x + 5) \: with \: (x + 3) \\ \\ \tt \: a = (x + 5) * (x + 3) \\ \tt \: a = x(x + 3) + 5(x + 3) \\ \tt \: a = {x}^(2) + 3x + 5x + 3 \\ \large \boxed{\boxed{ \bf \: a = {x}^(2) + 8x + 3}}`

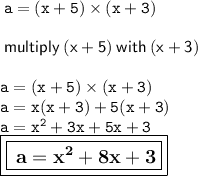
✯ Area of the rectangle = x² + 8x + 3 cm².

▨▧▨▧▨▧▨▧▨▧▨▧▨▧▨▧▨

Question 4 ↴

➜ Length of the side of a square = x + 6 cm

➜ Area of the square = a

﹋﹋﹋﹋﹋

✪ Area of a square = side × side

⇒ Area of a square = side²

⇒ a = (x + 6)²

﹋﹋﹋﹋﹋

WORKING ↷

`\tt \: a = (x + 6) ^(2) \\ \\ \sf \: Use \: the \: algebraic \: identity \downarrow \: \\ \sf (a + b) ^(2) = {a}^(2) + 2ab + {b}^(2) ... \\ \sf \: a = x \: and \: b = 6 \\ \\ \tt \: a = (x + 6) ^(2) \\ \tt \: a = {x}^(2) + 2 * x * 6 + {6}^(2) \\ \large \boxed{\boxed{ \bf \: a = {x}^(2) + 12x + 36}}`

✯ Area of the square = x² + 12x + 36 cm².

▨▧▨▧▨▧▨▧▨▧▨▧▨▧▨▧▨