Answer:
b = - 2, b = 4
Explanation:
Using the distance formula
d =
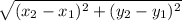
with (x₁, y₁ ) = M(3, 1) and (x₂, y₂ ) = N(- 1, b)
d =
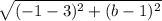
=
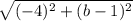
=
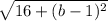
Then
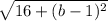 = 5 ( square both sides )
= 5 ( square both sides )
16 + (b - 1)² = 25 ( subtract 16 from both sides )
(b - 1)² = 9 ( take square root of both sides )
b - 1 = ±
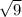 = ± 3 ( add 1 to both sides )
= ± 3 ( add 1 to both sides )
b = 1 ± 3
Then
b = 1 - 3 = - 2 or b = 1 + 3 = 4