Question

An investment producing cash flows in the amount of $1,200 per month is undertaken for a period of 28 months. The investor pays $24,000 for the investment and the contract stipulates that investment returns must be reported on a basis equivalent with annual compounding. Given that the investment is sold after 28 months, what would be the equivalent annual compound rate

Answer 1

To find the equivalent annual compound rate, calculate the ratio of the future value to the present value, raised to the power of 1 divided by the investment period in years, and subtract one from that result to get the rate.

Step-by-step explanation:

To calculate the equivalent annual compound rate for an investment with monthly cash flows, we need to find the rate at which the investment needs to compound annually to reach the total return received after 28 months. The investor paid $24,000 for the investment and received $1,200 per month for 28 months, resulting in total cash flows of $1,200 × 28 = $33,600. The total return is then $33,600 - $24,000 = $9,600.

Let r be the equivalent annual compound rate. The future value (FV) using annual compounding after t years is given by:

FV = PV ×
`(1 + r)^t`

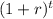
Where PV is the present value of the investment. We can rearrange the formula to solve for r:

(1 + r) =
`(FV/PV)^(1/t)`

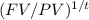
Since the investment lasts for 28 months, t in years is 28/12. Substituting the known values:

(1 + r) =
`($33,600 / $24,000)^(1/(28/12))`

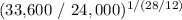
Calculating the right side of the equation gives us the value of (1 + r), from which we can then derive the r, the equivalent annual compound rate.

Answer 2

can u make it more understanding