Question

Peter invested ₱10,000 at the rate of 2% compounded annually, Which of the following represents the amount of his money after 10 years?​

a. A=10,000(1.2)
10
c. A=10,000(1.02)
10
b. A=10,000(12)
10
d.A=10,000(1.12)
10

Answer 1

₱12,189.94

Explanation:

Given the principal amount of ₱10,000, and an interest rate of 2% compounded annually:

We can use the Future Value formula to determine what the value of Peter's money will be after 10 years:

`FV = PV(1 + (r)/(n))^(n*t)`

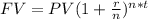
Where PV = present value of the principal = ₱10,000

r = interest rate = 2% or 0.02

n = number of compounding periods (annually) = 1

t = number of years = 10

Plug in the given values into the FV formula:

`FV = PV(1 + (r)/(n))^(n*t)`

`FV = 10000(1 + (0.02)/(1))^(1*10)`

`FV = 10000(1 + 0.02)^(10)`

`FV = 10000(1.02)^(10) = 10000(1.21899442)`

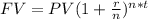
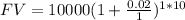
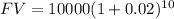
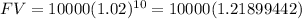
FV = ₱12,189.94

Therefore, the amount of Peter's money after 10 years is ₱12,189.94.