Question

If you draw one card from a standard deck, what is the probability of drawing a 5 or a diamond? Are the events inclusive or mutually exclusive?

Mutually Exclusive/Dependent
Inclusive/Independent

Answer 1

The probability of drawing number five or a card from the diamond suit is
`\displaystyle (4)/(13)`.

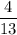These two events are mutually inclusive.

These two events are independent of one another.

Explanation:

There are
`52` distinct cards in a standard deck of cards.

There are
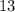`13` cards that are in the diamond suit. There is, however, one number five card in the diamond suit. There are
`3` cards that are numbered "five" but not in the diamond suit.

In total,
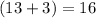`(13 + 3) = 16` of the
`52` cards in a standard deck would meet the requirements. If a card is drawn randomly, there is a
`(16 / 52)` probability that this card meets the requirements. This ratio simplifies to
`(4 / 13)`.

Drawing a "
`5`" and drawing a "diamond" could happen simultaneously with one draw- namely when a "
`5\!`" card from the diamond suit was drawn.

Hence, these two events are not mutually exclusive. Rather, they are mutually inclusive since they could happen at the same time.

Consider two events: event
`A` and event
`B`.

Let
`P(A)` and
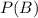`P(B)` denote the probabilities of each event, respectively. Let
`P(A \cap B)` denote the probability that the two event happen at the same time.

Event
`A` and event
`B` are independent events if and only if
`P(A) \, P(B) = P(A \cap B)`.

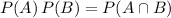In other words, two events are independent if and only if the product of the probabilities that the two events happen separately is equal to the probability that the two events simultaneously.

For example, in this question:

• The probability of drawing a "
  `5`" (event
  `A`) is
  `(4 / 52)`. which simplifies to
  `(1 / 13)`.
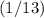• The probability of drawing a "diamond" (event
  `B`) is
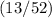  `(13 / 52)`, which simplifies to
  `(1/4)`.
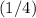• The probability of drawing a "
  `5`" and a "diamond" at the same time is
  `(1 / 52)`.

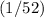The probabilities of the two events happening separately are
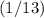`(1 / 13)` and
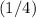`(1 / 4)` , respectively. The product of these two probabilities is
`P(A)\, P(B) = (1 / 4) * (1 / 13) = (1 / 52)`.

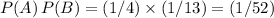On the other hand, the probability of the two events happening at the same time is
`P(A \cap B) = (1 / 52)`.

Thus,
`P(A)\, P(B) = P(A \cap B)`. Therefore, these two events (drawing a "
`5`" and drawing a "diamond") are independent of one another.