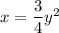Answer:
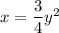
Explanation:
A graph with x-axis symmetry means that for every (x, y) point there is also a (x, -y) point on the graph, i.e. the x-axis acts like a mirror. Therefore, it is a sideways parabola.
The general form of this type of equation is
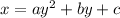
Since we know that the curve has a vertex of (0, 0) then
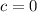
Therefore,
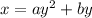
Given that (3, 2) is on the curve, then (3, -2) is also on the curve.
Substituting the given point (3, 2):
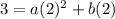
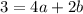
Substituting the given point (3, -2)
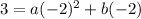
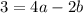
Adding the equations together to eliminate
 :
:
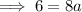
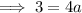
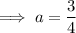
Therefore,
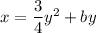
Again, substituting point (3, 2) means that b = 0
Therefore, the final equation is: