Question

Use
S=n2 to find the sum of 1+3+5+. . . + 301.

Answer 1

I'm not sure what the question means by "use S = n^2"...

At any rate, the given sum

1 + 3 + 5 + … + 301

is simply the sum of the first 151 odd positive integers, which we can write in the form 2n - 1 for n between 1 and 151. That is,

`1+3+5+\cdots+301 = \displaystyle\sum_(n=1)^(151)(2n-1)`

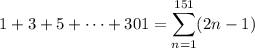
We can expand the sum as

`\displaystyle 2\sum_(n=1)^(151)n - \sum_(n=1)^(151)1`

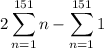
Next, recalling that

`\displaystyle \sum_(i=1)^n1 = 1+1+1+\cdots+1 = n \text{ and }\sum_(i=1)^ni=1+2+3+\cdots+n = \frac{n(n+1)}2`

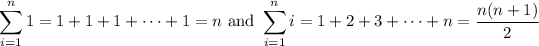
it follows that

`1+3+5+\cdots+301 = 2\cdot\frac{151\cdot152}2 - 151 = 151\cdot(152-1) = 151^2 = \boxed{22,801}`

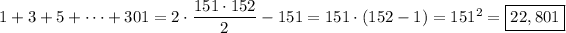
(Probably "S = n^2" means "sum of n odd integers = n ²")