Answer:
The maximum value of the objective function is 30 at (15, 0).
Explanation:
Given the objective function, F = 2x + y
and the following constraints:
3x + 5y ≤ 45
2x + 4y ≤ 32
x ≥ 0
y ≥ 0
You must first find the intercepts of the given constraints to plot the points on the graph, and find the feasible region.
3x + 5y = 45
3x + 5y - 3x = - 3x + 45
5y = -3x + 45
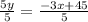
y = -3/5x + 9 (Slope-intercept form).
Solve for y-intercept by setting x = 0:
y = -3/5x + 9
y = -3/5(0) + 9
y = 9
y-intercept: (0, 9).
Solve for x-intercept by setting y = 0:
y = -3/5x + 9
0 = -3/5x + 9
0 - 9 = -3/5x + 9 - 9
- 9 = -3/5x
Multiply both sides by (-5/3) to isolate x:
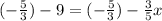
15 = x
x-intercept: (15, 0).
Next, transform 2x + 4y ≤ 32 into slope-intercept form, and solve for the y- and x-intercepts:
2x + 4y = 32
2x + 4y - 2x = - 2x + 32
4y = -2x + 32
Divide both sides by 4 to isolate y:
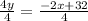
y = -1/2x + 8 (slope-intercept form)
Solve for y-intercept by setting x = 0:
y = -1/2x + 8
y = -1/2(0) + 8
y = 8
y-intercept: (0, 8).
Solve for x-intercept by setting y = 0:
y = -1/2x + 8
0 = -1/2x + 8
0 - 8 = -1/2x + 8 - 8
-8 = -1/2x
Divide both sides by -1/2 to solve for x:
-8 / -1/2 = (-1/2x)/ -1/2
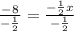
16 = x
x-intercept: (16, 0).
Now that you have the following points: (0, 9), (15, 0), (0, 8), and (16, 0), you can plot these on the graph and setup a feasible region. (Please see the attached screenshot for details.
The x-intercept, (16, 0) is not included because it is not within the feasible region.
You must also evaluate the objective function at each corner point to identify which is the maximum value.
Corner Point F = 2x + y
(0, 0) F = 2(0) + (0) = 0
(0, 8) F = 2(0) + (8) = 8
(0, 9) F = 2(0) + (9) = 9
(15, 0) F = 2(15) + (0) = 30
(10, 3) F = 2(10) + (3) = 23
Therefore, the maximum value of the objective function is 30 at (15, 0).