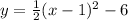Question

Identify the coordinates of the vertex of this parabola.

Answer 1

The coordinates of the vertex is (1, -6).

Explanation:

Given the parabola,
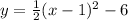`y = (1)/(2)(x - 1)^(2) - 6`, where a =
`(1)/(2)`, and the vertex is represented by (h, k) = (1, -6). Since it is an upward-facing parabola, the vertex is the minimum point in the graph.

I came up with the formula for the quadratic equation by using the coordinates for the vertex (1, -6) and the y-intercept, (0, -5.5) from the given graph. The y-intercept is the point in the graph where the parabola crosses the y-axis, and the value of its x-coordinate is 0.

I Plug the following values into the quadratic equation in vertex form:
`y = a(x - h)^(2) + k`.

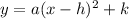Let y = -5.5

x = 0

h = 1

k = -6

Since we need to find the value of a:

`y = a(x - h)^(2) + k`

`-5.5 = a(0 - 1)^(2) - 6`

`-5.5 = a(- 1)^(2) - 6`

`-5.5 = 1a - 6`

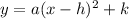
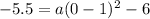
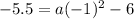
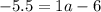
Add 6 to both sides to isolate 1a:

-5.5 + 6 = 1a - 6 + 6

0.5 = 1a

Divide both sides by 1 to solve for a:

`(0.5)/(1) = (1a)/(1)`

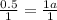
0.5 or 1/2 = a

The value of a determines whether the graph opens up or down. Since the value of a is positive, the graph of the parabola opens upward. Therefore, the formula of the parabola in vertex form is:

`y = (1)/(2)(x - 1)^(2) - 6`