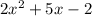Question

Let f(x) = 3x2 + 2x – 1 and g(x) = x2 – 3x + 1
Find f(x) - g(x)

Answer 1

1. subtract like terms
3x^2 - x^2 = 2x^2
2x - -3x = 5x
-1 - 1 = -2
2. combine final product

f(x) - g(x) = 2x^2 + 5x - 2

Answer 2

`\boxed {\boxed {\sf f(x)-g(x) = 2x^2 +5x-2}}`

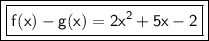
Explanation:

We are asked to find f(x) - g(x) or the difference between the two functions. We know that the functions are:

• f(x)= 3x² +2x -1
• g(x)= x² - 3x +1

We can substitute the expressions for the functions.

`f(x) - g(x)`

`(3x^2 +2x-1)- (x^2-3x+1)`

First, we must distribute the -1 in front of the second set of parentheses. Multiply each term inside the parentheses by -1.

`(3x^2+2x-1) + ( -1*x^2) + (-1* -3x) + (-1*1)`

`(3x^2+2x-1) + (-x^2)+ (3x) + (-1)`

`(3x^2+2x-1)+ (-x^2+3x-1)`

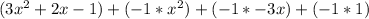
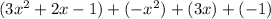
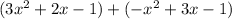
Now we can combine like terms. The terms with x² can be combined, then the terms with x, and finally the constants (terms without variables).

`(3x^2+ -x^2 ) + (2x+3x) + (-1+ -1)`

`(2x^2) + (5x) + (-2)`

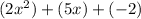
Eliminate any unnecessary addition signs and parentheses.

`2x^2+5x-2`