Question

Hello help me with this question thanks in advance​

Answer 1

`\bold{\huge{\underline{ Solution\: C }}}`

Part 5 :-

Here,

• Two non parallel lines are intersected by three parallel lines .
• These three parallel lines are also parallel to each other.

By using basic proportionality theorem

• It states that the line which is parallel to one side of triangle intersects the other two sides then the other two sides are divided in the same ratios.

That is,

`\sf{( x )/( x + 16 )}{\sf{=}}{\sf{(9)/(12 + 9)}}`

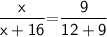
By cross multiplication ,

`\sf{ 21x = 9( x + 16)}`

`\sf{ 21x = 9x + 144}`

`\sf{ 21x - 9x = 144}`

`\sf{ 12x = 144}`

`\sf{ x = }{\sf{( 144)/(12)}}`

`\bold{ x = 12}`

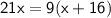
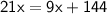
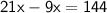
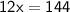
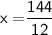
Hence, The value of x is 12

Part 6 :-

Here also ,

• Two non parallel lines are intersected by three parallel lines .
• These three parallel lines are also parallel to each other.

By using basic proportionality theorem :-

`\sf{( 4 )/( 4 + 10 )}{\sf{=}}{\sf{(6)/(x +6)}}`

`\sf{( 4 )/( 14 )}{\sf{=}}{\sf{(6)/(x +6)}}`

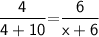
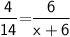
By cross multiplication ,

`\sf{ 4(x + 6) = 6 {*} 14}`

`\sf{ 4x + 24 = 84}`

`\sf{ 4x = 84 - 24}`

`\sf{ x = }{\sf{( 60)/(4)}}`

`\bold{ x = 15}`

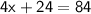
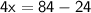
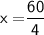
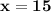
Hence, The value of x is 15 .

`\bold{\huge{\underline{ Solution\: D }}}`

Part 7 :-

Here,

• Here, JL bisects Angle J in ΔHJK
• It means Angle JHL = Angle JKL
• The length of HJ = 12 , JK = 15 , HL = 18

Therefore,

In triangle JHL and In triangle JKL

By using similarity theorem

• It states that if the two triangles are similar then the corresponding sides of triangle are in proportion and corresponding angles are equal

That is,

`\sf{( JH )/( JK)}{\sf{=}}{\sf{(HL)/(KL)}}`

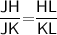
Subsitute the required values,

`\sf{( 12 )/( 15 )}{\sf{=}}{\sf{(18)/(KL)}}`

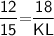
By cross multiplication

`\sf{ 12( KL) = 18 {*} 15}`

`\sf{ 12(KL) = 270}`

`\sf{ KL = }{\sf{( 270)/(12)}}`

`\bold{ KL = 22.5 }`

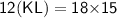
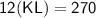
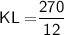
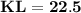
Hence, The length of KL is 22.5

Part 8 :-

Here also,

• Here, JL bisects Angle J in ΔHJK
• It means Angle JHL = Angle JKL
• The length of KL = 6 , JK = 20 , HJ = 14

Therefore,

In triangle JHL and In triangle JKL

By using similarity theorem :-

`\sf{( JH )/( JK)}{\sf{=}}{\sf{(HL)/(KL)}}`

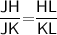
Subsitute the required values,

`\sf{( 14 )/( 20)}{\sf{=}}{\sf{(HL)/(6)}}`

`\sf{( 7 )/( 10)}{\sf{=}}{\sf{(HL)/(6)}}`

`\sf{( 7 )/( 10)}{\sf{{*} 6= HL }}`

`\sf{( 7 )/( 5 )}{\sf{{*} 3 = HL }}`

`\sf{( 21 )/( 5)}{\sf{ = HL }}`

`\bold{ HL = 4.2 }`

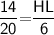
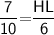
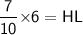
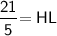
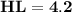
Hence, The length of HL is 4.2 .