Answer:
Correct answer: D) Center: (-3, 17), Radius: 13
Explanation:
Given the diameter of a circle with endpoints: (2, 5) (-8, 29):
Let
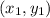 = (2, 5)
= (2, 5)
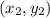 = (-8, 29)
= (-8, 29)
To find the center of the circle, we can use the Midpoint formula:
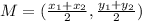
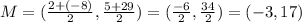
Therefore, the center of the circle is (-3, 17).
We can use the distance formula to find the actual distance between these endpoints, and to help determine the radius of the circle.
The distance formula is:
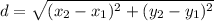

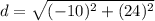

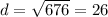
Therefore, the diamater of the circle is 26, which means that the radius is 13.