Answer:

Explanation:
We are asked to find the slope of a line. The slope of a line gives the steepness and direction of a line. It is "rise over run" or the change in y over the change in x.
The formula for calculating slope is:
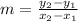
where (x₁, y₁) and (x₂, y₂) are the points the line passes through. The line passes through (0, -2) and (2, -4). If we match the values and their corresponding variable, we see that:
- x₁ = 0
- y₁ = -2
- x₂ = 2
- y₂= -4
Substitute the values into the formula.

Solve the numerator. Remember 2 back-to-back negative signs become a positive sign.
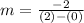
Solve the denominator.
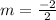
Divide.
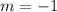
The slope of the line is -1 and choice A is correct.