Explanation:
Given:
Theater has 15 seats
Last Row has 72 seats.
Theater has a total of 870 seats.
Unknown: Number of rows
Number of seats in each row.
Equations: Since we know the total number of seats the Theater has we can use the sum of arithmetic series
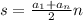
Where a1 is the first row of seats
s is total number of seats
an is last row of seats
n is number of rows.
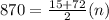
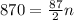
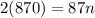
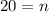
So we have 20 rows.
To find how many seats does each row increase, we use this formula,
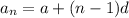
Let use the 20th row as an example,

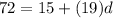
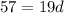
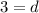
So the common difference is 3.
So the seats of each row increase by 3.