Given, equation of curve is
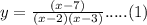
To find the intersection of given curve with X-axis, Put y = 0 in equation 1, we get,
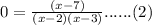
x − 7 = 0 ⟹ x = 7
Thus, the curve cut the X-axis at (7,0).
Now, on differentiating equation of curve w.r.t. x, we get,
![(dy)/(dx) \\ = \frac{(x - 2)(x - 3).1 - (x - 7)[(x - 2).1 + (x - 3).1]}{[(x-2)(x - 3) {}^(2)]}](https://img.qammunity.org/2022/formulas/mathematics/college/muvxbyvlz5cq671md8vnhebivo3haylymd.png)
Next answer is in pic.