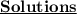
Figure 1 :-
Given :-
- We have one composite figure that is composed rectangle and triangle
- The dimensions of rectangle are 12 cm and 14 cm
- The dimensions of triangle are 12cm and 8cm
To Find :-
- We have to find the area of composite figure
Let's Begin :-
We have,
- Composite figure composed of rectangle and triangle
We know that,
Area of rectangle

- The dimensions of rectangle are 12cm and 14cm
Subsitute the required values,
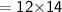

For triangle
Area of triangle

Subsitute the required values,
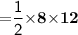
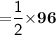
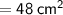
Thus, Area of triangle is 48 cm² .
Therefore,
The total area of the composite figure
= Area of rectangle + Area of triangle
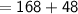
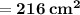
Hence, The area of given composite figure is 216 cm²
Figure 2 :-
Given :-
- We have one composite figure which is composed of semicircle and rectangle
- The dimensions of rectangle are 10 in. and 15 in.
- The diameter of semicircle is 10 in.
Let's Begin :-
Here, we have
- Composite figure composed of rectangle and hemisphere
We know that,
Area of rectangle

- The dimensions of rectangle are 10in. and 15 in.
Subsitute the required values,
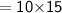
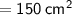
For hemisphere
Area of semicircle
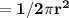
- The diameter of hemisphere is 10 in.
- So, The radius of hemisphere will be 5 in. as it is the half of diameter.
Subsitute the required values,
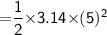
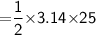
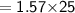
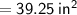
Thus, The area of semicircle is 39.25 in².
Therefore,
Total area of the given composite figure
= Area of hemisphere + Area of rectangle
=
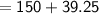
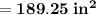
Hence, The total area of the given composite figure is 189.25 in² .