Answer:
Car B will be travelling after the crash at a constant speed of 20 mph in the same direction as Car A was travelling before the crash
Step-by-step explanation:
Let
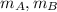 be the mass of car A resp. car B,
be the mass of car A resp. car B,
 the velocity of car A before the crash,
the velocity of car A before the crash,
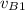 the velocity of car B after the crash. For car B being at rest before the crash and car A at rest after, it holds
the velocity of car B after the crash. For car B being at rest before the crash and car A at rest after, it holds
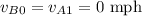 .
.
With conservation of momentum, it holds
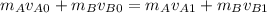
Zero terms eliminated:
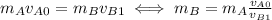
With conservation of energy and assuming that no conversion of mechanical energy into other forms of energy occurs (through friction etc.), the mechanical energy before and after the crash is simply equated:
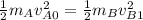
Inserting the
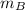 from above:
from above:
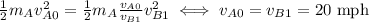
Bonus:
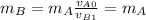 (both cars have the same weight)
(both cars have the same weight)