Question

A cylinder has radius 2.5 meters. its volume is 50pi meters. Find its height.

Answer 1

• 8 meters .

⠀

Explanation :

• The volume of the cylinder is 50π cubic meters.

• The cylinder has radius 2.5 meters.

⠀

To Find :

• The height of the cylinder.

⠀

Solution :

⠀

We know,

`{ \longrightarrow\qquad \bf\pi {r}^(2)h = \bf{Volume_((cylinder) ) }}`

⠀

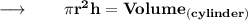
Where,

• r is the radius of the cylinder.
• h is the height of the cylinder.

⠀

Now, Substituting the values :

`{ \longrightarrow\qquad \sf\pi * {(2.5)}^(2) * h = {50 \pi } }`

`{ \longrightarrow\qquad \sf\pi * 6.25 * h = {50 \pi } }`

⠀

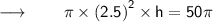
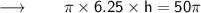
Cancelling π from both sides :

`{ \longrightarrow\qquad \sf \cancel\pi * 6.25 * h = {50 \: \cancel \pi } }`

`{ \longrightarrow\qquad \sf 6.25 * h = {50 } }`

`{ \longrightarrow\qquad \sf h = { (50)/(6.25) } }`

`{ \longrightarrow\qquad {\pmb {\bf{h = {8 } }}}}`

⠀

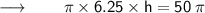
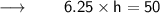
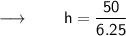
Therefore,

• The height of the cylinder is 8 meters .