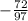Question

Given that tan θ= -65/72 and that angle θ terminates in quadrant II, then what is the value of cos θ?

Answer 1

cosθ =
`-(72)/(97)`

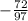
Explanation:

tanθ = -(65/72)

If it is in the 2nd quadrant, this means that y is positive but x is negative

tanθ= opposite/adjacent or (y/x)

tanθ=
`(65)/(-72)`

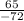
We know that the adjacent value = -72 and the opposite value = 65

The hypotenuse can be get by the following

`√((65)^2+(-72)^2) = 97`

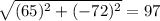
cosθ is just adjacent/hypotenuse

Our adjacent value is -72

Our hypotenuse is 97, therefore

cosθ =
`-(72)/(97)`