Question

Here are the three triangles for the last question!

Answer 1

Answer to Question #13

See the analysis

`Petermine\ the\ opposite\ side\\ to\ the\ angle\ and\ the\ adjacent\\ Side`

`tan\propto=(opposite)/(adjacent)`

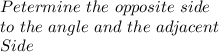
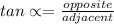
Answer to Question #11

Answer: see the analysis.

`Solution:\\ The\ sine\ of\ an\ angle\ is\ the\ ratio\ of\ Opposite\ to\ Hypotenuse.\\ So,\ we\ can\ use\ the\ formula\ sin(\theta)=(Opposite)/(Hypotenuse)to\ calculate\ the\ sine\ of\\ an\ angle\ in\ a\ right\ triangle.`

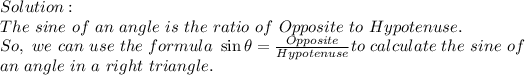
Answer to Question that asked "How would your results change if you used Angle B Instead of Angle A?"

Ans No Change

`Ans\ No\ change\\ After\ changing\ A\ to\ B\ no\ change\ will\\ be\ there`

Answer to Question #12

the ansurer is

cose C = Base/Hypitenuse = BC/AC

`Solution:\\ cosine\ of\ angle\ is\ the\\ Natis\ of\ base\ to\ the\\ lypotenuse\ of\ the\ friangle\\ cos\ C=(BC)/(AC)`

I hope this helps you!

:)