Answer to Question #13
See the analysis
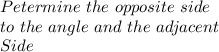
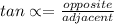
Answer to Question #11
Answer: see the analysis.
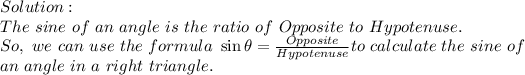
Answer to Question that asked "How would your results change if you used Angle B Instead of Angle A?"
Ans No Change
Answer to Question #12
the ansurer is
cose C = Base/Hypitenuse = BC/AC

I hope this helps you!
:)