Question

3. By using the properties of determinant, evaluate the following if​

Answer 1

a. We have
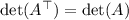`\det(A^\top) = \det(A)` for any square matrix A, so the determinant is the same, 10.

b. If a row or column is multiplied by some number, then the determinant of that matrix is equal to that number times the determinant of the original matrix. In this case, the second row is multiplied by 3 and the third row by 2, so the determinant is 2•3•10 = 60.

c. The same property in (b) is involved here (first row multiplied by -1, second by 3) but the second and third columns have been swapped relative to the original matrix. When rows or columns get permuted like this, the value of the determinant changes by a power of (-1). The power depends on how many tranpositions are needed to recover the original matrix.

`\begin{vmatrix}-a&-c&-b\\3d&3f&3e\\g&i&h\end{vmatrix} = -3\begin{vmatrix}a&c&b\\d&f&e\\g&i&h\end{vmatrix} = 3\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}`

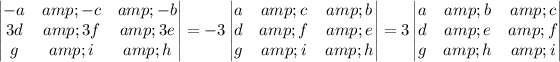
and we end up with a determinant of 3•10 = 30.